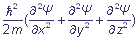Russian

SCHROEDINGER EQUATION

If we must define energy of steady states of an electronic system, the fundamental equation which was introduced by E. Schroedinger, serves for this. This equation relates the energy of a system to a wave function. In the simplest form, for a single electron, the Schroedinger equation has the form:

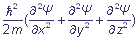- + U(x, y, z) Ψ = E · Ψ, where

U(x, y, z) is the potential energy of an electron;
Ψ is the wave function;
E is the total energy of the system in the steady state;
m is the mass of the electron;
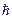is the Plank constant.

In a concise form, the Schroedinger steady-state equation can be written as Ψ = EΨ, where is a complete Hamiltonian.

Another form of the Schroedinger equation is: 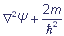(E - U) Ψ = 0, where ² is a Laplacian.

The Schroedinger equation possesses a solution not with any value of total energy of the system, but with some of them, which are called characteristic values. The complex of characteristic values of energy is called spectrum.

While non-stationary problems are considered, the dependence of a wave function on time Ψ = Ψ(x, y, z, t) is defined by the Schroedinger temporal equation:

i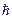 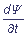= Ψ.

If does not depend on time, then the Schroedinger temporal equation has the solution of the following form:

         Ψ(x, y, z, t) = Ψ(x, y, z)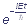      (1)
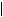        Ψ(x, y, z, t)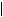² = Ψ(x, y, z) · Ψ^*(x, y, z, t) = 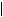Ψ(x, y, z)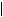², where
Ψ^* is a function, which is complex-conjugate to Ψ.

Thus, the function (1) also describes a stationary state, despite the fact that it includes time t. t.