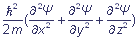English

УРАВНЕНИЕ ШРЕДИНГЕРА

Для определения энергии стационарных состояний электронной системы служит фундаментальное уравнение, которое ввел Э.Шредингер. Оно связывает энергию системы с волновой функцией. В простейшей форме для одного электрона уравнение Шредингера имеет вид:

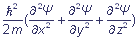- + U(x, y, z) Ψ = E · Ψ, где

U(x, y, z) - потенциальная энергия электрона;
E - полная энергия системы в стационарном состоянии;
Ψ - волновая функция;
m - масса электрона;
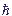- постоянная Планка.

В сокращенном виде стационарное уравнение Шредингера может быть записано как Ψ = EΨ, где - полный гамильтониан.

Другая форма записи уравнения Шредингера: 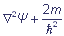(E - U) Ψ = 0, где ² - лапласиан.

Уравнение Шредингера имеет решение не при любых значениях полной энергии системы, а лишь при некоторых, называемых собственными значениями. Совокупность собственных значений энергии называется спектром.

При рассмотрении нестационарных задач зависимость волновой функции от времени Ψ = Ψ(x, y, z, t) определяется временным уравнением Шредингера:

i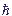 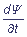= Ψ.

Если не зависит от времени, то временнóе уравнение Шредингера имеет решение вида

         Ψ(x, y, z, t) = Ψ(x, y, z)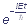      (1)
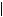        Ψ(x, y, z, t)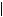² = Ψ(x, y, z) · Ψ^*(x, y, z, t) = 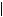Ψ(x, y, z)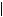², где
Ψ^* - функция, комплексно сопряженная Ψ.

Таким образом, функция (1) также описывает стационарное состояние, несмотря на то, что в нее входит время t.