E + S
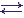 (ES)
(ES)  E + P, where
E + P, where
k-1
MICHAELIS-MENTEN EQUATION
The simplest enzymatic reaction is considered. One substrate (S) and one enzyme (E) participate in it, and one product (P) appears as the result of desintegration of the enzyme-substrate complex (ES):
k1 k2
E + S 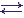 (ES)
(ES)  E + P, where
E + P, where
k-1
k1, k-1 - are the constants of the rates of the direct and counter reactions of the formation of the enzyme-substrate complex; k2 - is the constant of the rate of the product formation.
This system is described by the following differential equations:
 = - k1[S] · [E] + k-1[ES],
= - k1[S] · [E] + k-1[ES],
 = - k1[S] · [E] + k-1[ES] + k2[ES],
= - k1[S] · [E] + k-1[ES] + k2[ES],
 = - k1[S] · [E] - k-1[ES] - k2[ES], (1)
= - k1[S] · [E] - k-1[ES] - k2[ES], (1)
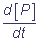 = k2[ES] = νP, where
= k2[ES] = νP, where
νP - is the rate of the product P formation P,
[E], [S], [ES], [P] - are the concentrations of the enzyme, substrate, enzyme-substrate complex and the final product correspondingly.
As the system preserves constant general concentration of enzyme E0, so at any time the sum of concentrations of the free enzyme and bonded enzyme is equal to [E] + [ES] = E0.
Characteristic lifetime τÅ of the variables [E] and [ES] is defined by the quickest stage of its desintegration with formation of the product PP, that is, the constant rate νP of the product formation: τÅ = 1/k2. The constant k2 corresponds to the number of catalytic actions, that is, to the number of the actions of desintegration of ES and formation of P in a unit of time. The time τÅ is the time of the enzyme circulation, and the constant k2 is called the number of enzyme circulations.
Characteristic time τS of decrease of S in the system and corresponding appearance of P depends on the rate of product formation: τS = S/νp. Maximal rate of the product formation will be achieved, when the whole amount of enzyme E0 is in bonded state: νpmax = k2·E0. So, τSmax = S/(k2·E0). Under usual conditions the concentration of the substrate S exceeds manifold the concentration of the product, that is, E/S ~ 10-4 << 1. That is why
τS >> τE, (2)
It means that [E] and [ES] are fast varying variables. Their changes are so fast, that they stay all the time around their stationary values. Consequently, they can be described by algebraic equations, which result from equalization to zero the right parts of the second and third equations in the model (1):
 =
=  = 0 (3).
= 0 (3).
If the conditions (2) and (3) are met, the Michaelis-Menten equation, which is well-known in biochemistry, comes out. The Michaelis-Menten equation is the equation of relationship of the stationary rate of an enzymatic reaction on the concentration of the substrate
νp = 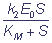 , where
, where
KM = 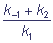 is the Michaelis constant.
is the Michaelis constant.