E + S
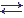 (ES)
(ES)  E + P, где
E + P, где
k-1
УРАВНЕНИЕ МИХАЭЛИСА-МЕНТЕН
Рассматривается простейшая ферментативная реакция, в которой участвуют один субстрат (S) и один фермент (E) и появляется один продукт (P) при распаде фермент-субстратного комплекса (ES):
k1 k2
E + S 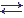 (ES)
(ES)  E + P, где
E + P, где
k-1
k1, k-1 - константы скоростей прямой и обратной реакций образования фермент-субстратного комплекса; k2 - константа скорости образования продукта.
Эта система описывается следующими дифференциальными уравнениями:
 = - k1[S] · [E] + k-1[ES],
= - k1[S] · [E] + k-1[ES],
 = - k1[S] · [E] + k-1[ES] + k2[ES],
= - k1[S] · [E] + k-1[ES] + k2[ES],
 = - k1[S] · [E] - k-1[ES] - k2[ES], (1)
= - k1[S] · [E] - k-1[ES] - k2[ES], (1)
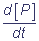 = k2[ES] = νP, где
= k2[ES] = νP, где
νP - скорость образования продукта P,
[E], [S], [ES], [P] - концентрации соответственно фермента, субстрата, фермент-субстратного комплекса и конечного продукта.
Поскольку в системе сохраняется постоянной общая концентрация фермента E0, то в любой момент времени сумма концентраций свободного и связанного фермента равна [E] + [ES] = E0.
Характерное время τЕ жизни переменных [E] и [ES] определяется наиболее быстрой стадией его распада с образованием продукта P, т.е. константой скорости νP образования продукта: τЕ = 1/k2. Константа k2 соответствует числу актов катализа, т.е. числу актов распада ES и образования P в единицу времени. Время τЕ - это время оборота фермента, а константа k2 называется числом оборотов фермента.
Характерное время τS убыли S в системе и соответствующего появления P зависит от скорости образования продукта: τS = S/νp. Максимальная скорость образования продукта будет достигнута, когда весь фермент E0 находится в связанном состоянии: νpmax = k2·E0. Значит, τSmax = S/(k2·E0). В обычных условиях концентрация субстрата S во много раз превышает концентрацию продукта, т.е. E/S ~ 10-4 << 1. Поэтому
τS >> τE, (2)
а это означает, что [E] и [ES] являются быстрыми переменными. Их изменения настолько быстры, что они пребывают все время около своих стационарных значений. Следовательно, их можно описывать алгебраическими уравнениями, которые получаются путем приравнивания к нулю правых частей второго и третьего уравнения в модели (1):
 =
=  = 0 (3).
= 0 (3).
При выполнении условий (2) и (3) получается известное в биохимии уравнение Михаэлиса-Ментен зависимости стационарной скорости ферментативной реакции от концентрации субстрата
νp = 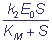 , где
, где
KM = 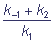 - константа Михаэлиса.
- константа Михаэлиса.