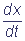 = AF(x,y),
= AF(x,y),
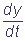 = Q(x,y),
where
= Q(x,y),
where
FAST VARYING VARIABLE
Assume that we have two differential equations for two variables x and y, that
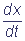 = AF(x,y),
= AF(x,y),
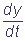 = Q(x,y),
where
= Q(x,y),
where
A >> 1 is a larger value. It means that the product AF(x,y) is a larger value, and, consequently, the rate of change is also the larger one. Hence it follows that x is a fast varying variable. Designate and divide the right and left parts to A. We obtain
ε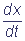 = F(x,y),
= F(x,y),
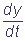 = Q(x,y), where
= Q(x,y), where
ε << 1. (ε = 1/A).
It can be seen that if
ε → 0 ε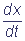 = F(x,y) = 0.
= F(x,y) = 0.
It means that the differential equation for the variable x can be replaced by algebraic one F(x,y) = 0, in which x takes the stationary value, which depends on y as a parameter, that is x = x(y).
In this sense the slow variable y is the governing parameter, and one can influence the coordinates of the stationary point x(y). by varying the governing parameter.