Russian
STOCHASTIC ELECTRON TRANSFER MODELS
I. Electron transfer model in shuttle molecule complexes localized in energy-conjugated
mitochondrial membranes and photosynthesizing organelles -
chloroplasts of plants and chromatophores of photosynthesizing bacteria.
Elementary transitions of an
electron between individual states of a multi-enzymatic complex can be in the first approximation considered as Markovian process, that is, probabilities of transitions between individual states i and j of the multi-enzymatic complex in every moment of time can be characterized of certain numbers kij that do not depend on the prehistory of the system.
Let S1, S2, …, Sn be states of the multi-enzymatic complex, and the probability that the complex is in the condition Si in the moment of time t: p (Si, t) = pi(t), i=1,2,…, n.
For every moment of time
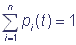 ,
because the multi-enzymatic complex is necessarily in one of the introducing states, but cannot be in two different states at the same time.
,
because the multi-enzymatic complex is necessarily in one of the introducing states, but cannot be in two different states at the same time.
If the complex is in the i-th state in the moment of time t, then the probability of its transfer into the j-th state during the period of time Δt can be expressed as aijΔt, i≠ j.. Here aij is the transition velocity constant, aij≥0, i≠ j. The probability that the complex will remain in the initial state after Δt is 1- aiΔt, where the value ai complies with the equality ai=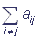 .
.
If in the moment of time t the system was in the i-th state, then in the moment of time (t + Δt) it will either remain in the initial state (with probability aijΔt), or will transfer in one of the n-1 remaining possible states (with probability aijΔt).
Sending Δt to zero, we will come to the following system of linear differential equations:
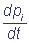 = - aipi +
= - aipi +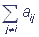 pj, pi(0) = ci ≥0;
pj, pi(0) = ci ≥0; 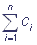 =1.
=1.
II. The described model does not take into consideration presence of mobile shuttles of electrons in some regions of the electron-transport chain. In mathematical description of an electron transfer, differences in the organization of individual regions of electron transport must be taken into account. In the case when shuttles of electrons are mobile enough to interact with one another by encounters, reductive-oxidative states of individual shuttles can be considered as independent. In accordance with the
mass action law, for the reaction of electron transfer between two one-electron shuttles C1 and C2 interacting by the scheme
k1 k2 k3
D → C1 → C2 → A, (1)
kinetic equations describing the studied reductive-oxidative reactions can be written in the form
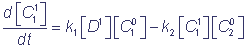
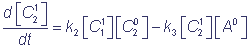 ,
,
where
 D1
D1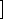 ,
, 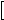 C11
C11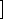 ,
, 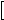 C21
C21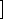 are concentrations of the reduced form of the exogenous donor D and the electron shuttles C1 and C2;
are concentrations of the reduced form of the exogenous donor D and the electron shuttles C1 and C2;
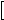 C10
C10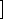 ,
, 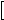 C20
C20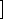 ,
, 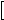 A0
A0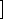 are concentrations of the oxidated form of the shuttles C1, C2 and the exogenous acceptor A; k1, k2, k3 are bimolecular constants of the velocities of the corresponding reactions.
are concentrations of the oxidated form of the shuttles C1, C2 and the exogenous acceptor A; k1, k2, k3 are bimolecular constants of the velocities of the corresponding reactions.
III. Unlike the case of reductive-oxidative reactions in a solution, when every reduced molecule of the shuttle C1 could pass an electron to any oxidated molecule C2, in a complex the reduced shuttle C1 can interact only with the oxidated shuttle C2, which is in the same complex with C1. To describe an electron transfer in a complex, all states, in which this complex can be, must be considered. The states of the complex can be defined as an ordered collection of states of shuttles, which constitute the complex. As this takes place, every shuttle in the complex can be either in the reduced, or the oxidated form, either in the protonated, or deprotonated state, and so on.
Let us designate the states of the complex as S1, S2, …, Sn and introduce the probability that the shuttle complex is in the state Si in the moment of time t: p(Si, t) = pi(t), i = 1, 2, …, n. The events S1, S2, …, Sn are incompatible and form the full group of the events, that is why the normalization requirement 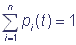 is fulfilled. If transitions between the states Si of the shuttle complex are viewed as Markovian process with a finite number of states and continuous time, then transitions of the complex from one state to another are described by a system of linear ordinary differential equations relative to probabilities:
is fulfilled. If transitions between the states Si of the shuttle complex are viewed as Markovian process with a finite number of states and continuous time, then transitions of the complex from one state to another are described by a system of linear ordinary differential equations relative to probabilities:
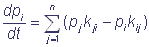 ; pi(0) = bi (i = 1, 2, ..., n), where bi are initial values of the probabilities of the corresponding states.
On examination particular electron-transport chains it is convenient to present a state of a complex in the form of a marked graph, in the vertices of which the states of the complex are placed, and arrows show possible transition between the states. In particular, for electron transfer in a complex of two shuttles on the chart (1) the marked graph of the states has the following form:
; pi(0) = bi (i = 1, 2, ..., n), where bi are initial values of the probabilities of the corresponding states.
On examination particular electron-transport chains it is convenient to present a state of a complex in the form of a marked graph, in the vertices of which the states of the complex are placed, and arrows show possible transition between the states. In particular, for electron transfer in a complex of two shuttles on the chart (1) the marked graph of the states has the following form:
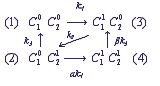 (2)
(2)
Here upper indices 0 and 1 designate presence or absence of an electron on the corresponding shuttle.
The numbers in brackets show the numbers of the complex states, ki are velocity constants of the corresponding transitions, marked on the chart (1). In the general case velocity constants of transitions between the states of the complex can depend on states of the shuttles, which do not participate immediately in the reaction (cooperativity effect). The parameters α and β characterize the degree of cooperativity. For example, the velocity of electron inflow from the inner donor to the shuttle C1 can be different, depending on the redox-state of the shuttle C2 (α≠1). The following system of differential equations for the probabilities of the states of the complex C1C2 describes the functioning of the complex according to the chart (2), at α = β = 1:
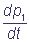 = k3 p2 - k1 p1;
= k3 p2 - k1 p1;
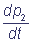 = k2 p3 - (k1 + k3) p2;
= k2 p3 - (k1 + k3) p2;
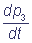 = k1 p1 + k3 p4 - k2 p3;
= k1 p1 + k3 p4 - k2 p3;
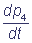 = k1 p2 - k3 p4; pi(0) = bi.
= k1 p2 - k3 p4; pi(0) = bi.
After solving this system of equations relative to the probabilities of the states of the complex pi, it is easy to find also the probabilities of the states of individual shuttles. For example, the probability that the first shuttle is in the oxidated state
p(C10) = p(C10C20) + p(C10C21) = p1 + p2 = 1- p(C11).
.
The equations, which describe transitions between states of a multi-enzymatic complex, are linear. However, the number of these equations quickly increases with increasing of the number of shuttles. For a complex of n shuttles, where each of the shuttles can be either oxidated or reduced, the number of states is equal to 2n.
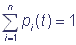 ,
because the multi-enzymatic complex is necessarily in one of the introducing states, but cannot be in two different states at the same time.
,
because the multi-enzymatic complex is necessarily in one of the introducing states, but cannot be in two different states at the same time.
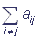 .
.
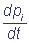 = - aipi +
= - aipi +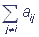 pj, pi(0) = ci ≥0;
pj, pi(0) = ci ≥0; 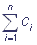 =1.
=1.
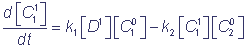
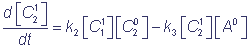 ,
,
 D1
D1 ,
, 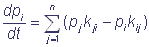 ; pi(0) = bi (i = 1, 2, ..., n), where bi are initial values of the probabilities of the corresponding states.
On examination particular electron-transport chains it is convenient to present a state of a complex in the form of a marked graph, in the vertices of which the states of the complex are placed, and arrows show possible transition between the states. In particular, for electron transfer in a complex of two shuttles on the chart (1) the marked graph of the states has the following form:
; pi(0) = bi (i = 1, 2, ..., n), where bi are initial values of the probabilities of the corresponding states.
On examination particular electron-transport chains it is convenient to present a state of a complex in the form of a marked graph, in the vertices of which the states of the complex are placed, and arrows show possible transition between the states. In particular, for electron transfer in a complex of two shuttles on the chart (1) the marked graph of the states has the following form:
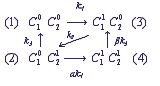 (2)
(2)
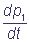 = k3 p2 - k1 p1;
= k3 p2 - k1 p1;
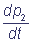 = k2 p3 - (k1 + k3) p2;
= k2 p3 - (k1 + k3) p2;
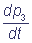 = k1 p1 + k3 p4 - k2 p3;
= k1 p1 + k3 p4 - k2 p3;
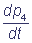 = k1 p2 - k3 p4; pi(0) = bi.
= k1 p2 - k3 p4; pi(0) = bi.