English
ВЕРОЯТНОСТНЫЕ МОДЕЛИ ПЕРЕНОСА ЭЛЕКТРОНА
I. Модель переноса электрона
в комплексах молекул-переносчиков, локализованных в энергосопряженных мембранах митохондрий и фотосинтезирующих органелл - хлоропластов растений и хроматофоров фотосинтезирующих бактерий.
Элементарные переходы электрона между отдельными состояниями мультиферментного комплекса в первом приближении можно считать марковским процессом – т.е. вероятности переходов между отдельными состояниями i и j мультиферментного комплекса в каждый момент времени можно характеризовать некоторыми числами kij, не зависящими от предыстории системы.
Пусть S1, S2, …, Sn – состояния мультиферментного комплекса и вероятность того, что комплекс находится в состоянии Si в момент времени t: p (Si, t) = pi(t), i=1,2,…, n.
Для любого момента времени
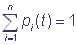 ,
потому что мультиферментный комплекс обязательно находится в одном из введенных состояний, но не может одновременно находится в двух разных состояниях.
,
потому что мультиферментный комплекс обязательно находится в одном из введенных состояний, но не может одновременно находится в двух разных состояниях.
Если комплекс находится в i-ом состоянии в момент времени t, то вероятность его перехода в j-ое состояние за время Δt может быть выражена как aijΔt, i≠ j. Здесь aij - константа скорости перехода, aij≥0, i≠ j. Вероятность того, что через Δt комплекс останется в исходном состоянии есть 1- aiΔt, где величина ai удовлетворяет равенству ai=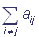 .
Если в момент времени t система находилась в i-ом состоянии, то в момент времени (t + Δt) она либо останется в исходном состоянии (с вероятностью 1- aiΔt), либо прейдет в одно из n-1 остальных возможных состояний (с вероятностью aijΔt):
.
Если в момент времени t система находилась в i-ом состоянии, то в момент времени (t + Δt) она либо останется в исходном состоянии (с вероятностью 1- aiΔt), либо прейдет в одно из n-1 остальных возможных состояний (с вероятностью aijΔt):
pi(t + Δt) = Δt·(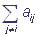 pj(t)) + (1- ai Δt) pi(t).
pj(t)) + (1- ai Δt) pi(t).
Устремляя Δt к нулю, придем к следующей системе линейных дифференциальных уравнений:
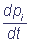 = - aipi +
= - aipi +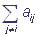 pj, pi(0) = ci ≥0;
pj, pi(0) = ci ≥0; 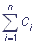 =1.
=1.
II. Описанная модель не учитывает наличие в некоторых участках электрон-транспортной цепи подвижных переносчиков электронов. При математическом описании переноса электрона следует учитывать различия в организации отдельных участков электронного транспорта. В том случае, когда переносчики электрона достаточно подвижны для того, чтобы взаимодействовать друг с другом посредством соударений, окислительно-восстановительные состояния отдельных переносчиков можно считать независимыми. В соответствии с законом действующих масс для реакции переноса электрона между двумя одноэлектронными переносчиками C1 и C2, взаимодействующими по схеме
k1 k2 k3
D → C1 → C2 → A, (1)
кинетические уравнения, описывающие рассматриваемые окислительно-восстановительные реакции, могут быть записаны в виде
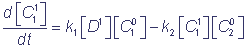
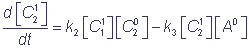 , где
, где
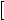 D1
D1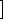 ,
, 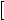 C11
C11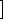 ,
, 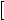 C21
C21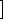 - концентрации восстановленной формы экзогенного донора D и переносчиков электронов C1 и C2;
- концентрации восстановленной формы экзогенного донора D и переносчиков электронов C1 и C2; 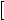 C10
C10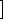 ,
, 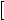 C20
C20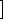 ,
, 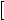 A0
A0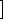 - концентрации окисленной формы переносчиков C1, C2 и экзогенного акцептора A; k1, k2, k3 - бимолекулярные константы скоростей соответствующих реакций.
- концентрации окисленной формы переносчиков C1, C2 и экзогенного акцептора A; k1, k2, k3 - бимолекулярные константы скоростей соответствующих реакций.
III. В отличие от случая окислительно-восстановительных реакций в растворе, когда каждая восстановленная молекула переносчика C1 могла отдать электрон любой окисленной молекуле C2, в комплексе восстановленный переносчик C1 может взаимодействовать только с тем окисленным переносчиком C2, который находится с C1 в одном комплексе. Для описания переноса электрона в комплексе необходимо рассматривать все состояния, в которых может находиться этот комплекс. Состояния комплекса могут быть определены как упорядоченная совокупность состояний переносчиков, составляющих комплекс. При этом каждый из переносчиков, входящих в комплекс, может находиться в окисленной и восстановленной форме, в протонированном или депротонированном состоянии и т.д.
Обозначим состояния комплекса через S1, S2, …, Sn и введем вероятность того, что комплекс переносчиков находится в состоянии Si в момент времени t: p(Si, t) = pi(t), i = 1, 2, …, n. События S1, S2, …, Sn несовместны и образуют полную группу событий, поэтому выполняется условие нормировки 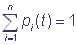 . Если рассматривать переходы между состояниями Si комплекса переносчиков как марковский процесс с конечным числом состояний и непрерывным временем, то переходы комплекса из одного состояния в другое описываются системой линейных обыкновенных дифференциальных уравнений относительно вероятностей:
. Если рассматривать переходы между состояниями Si комплекса переносчиков как марковский процесс с конечным числом состояний и непрерывным временем, то переходы комплекса из одного состояния в другое описываются системой линейных обыкновенных дифференциальных уравнений относительно вероятностей:
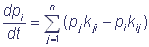 ; pi(0) = bi (i = 1, 2, ..., n), где bi - начальные значения вероятностей соответствующих состояний.
; pi(0) = bi (i = 1, 2, ..., n), где bi - начальные значения вероятностей соответствующих состояний.
При рассмотрении конкретных электрон-транспортных цепей удобно представлять состояния комплекса в виде размеченного графа, в вершинах которого стоят состояния комплекса, а стрелки указывают возможные переходы между состояниями. В частности, для переноса электронов в комплексе из двух переносчиков на схеме (1) размеченный граф состояний будет иметь следующий вид:
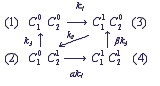 (2)
(2)
Здесь верхние индексы 0 и 1 означают отсутствие или наличие электрона на соответствующем переносчике. Цифры в скобках указывают номер состояния комплекса, ki – константы скоростей соответствующих переходов, указанных на схеме (1). В общем случае константы скоростей перехода между состояниями комплекса могут зависеть от состояний переносчиков, не принимающих непосредственного участия в реакции (эффект кооперативности). Параметры α и β характеризуют степень кооперативности. Например, скорость притока электронов от внешнего донора на переносчик C1 может быть различной в зависимости от редокс-состояния переносчика C2 (α≠1). Система дифференциальных уравнений для вероятностей состояний комплекса C1C2, описывающая его функционирование согласно схеме (2), при α = β = 1 имеет вид:
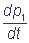 = k3 p2 - k1 p1;
= k3 p2 - k1 p1;
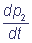 = k2 p3 - (k1 + k3) p2;
= k2 p3 - (k1 + k3) p2;
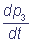 = k1 p1 + k3 p4 - k2 p3;
= k1 p1 + k3 p4 - k2 p3;
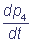 = k1 p2 - k3 p4; pi(0) = bi.
= k1 p2 - k3 p4; pi(0) = bi.
Решив эту систему уравнений относительно вероятностей состояний комплекса pi, легко найти и вероятности состояний отдельных переносчиков. Например, вероятность того, что первый переносчик находится в окисленном состоянии
p(C10) = p(C10C20) + p(C10C21) = p1 + p2 = 1- p(C11).
Уравнения, описывающие переходы между состояниями мультиферментного комплекса, линейны. Однако число этих уравнений быстро увеличивается с ростом числа переносчиков. Для комплекса из n переносчиков, каждый из которых может быть окисленным или восстановленным, число состояний равно 2n.
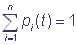 ,
потому что мультиферментный комплекс обязательно находится в одном из введенных состояний, но не может одновременно находится в двух разных состояниях.
,
потому что мультиферментный комплекс обязательно находится в одном из введенных состояний, но не может одновременно находится в двух разных состояниях.
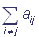 .
Если в момент времени t система находилась в i-ом состоянии, то в момент времени (t + Δt) она либо останется в исходном состоянии (с вероятностью 1- aiΔt), либо прейдет в одно из n-1 остальных возможных состояний (с вероятностью aijΔt):
.
Если в момент времени t система находилась в i-ом состоянии, то в момент времени (t + Δt) она либо останется в исходном состоянии (с вероятностью 1- aiΔt), либо прейдет в одно из n-1 остальных возможных состояний (с вероятностью aijΔt):
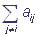 pj(t)) + (1- ai Δt) pi(t).
pj(t)) + (1- ai Δt) pi(t).
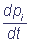 = - aipi +
= - aipi +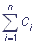 =1.
=1.
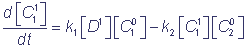
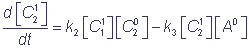 , где
, где
 D1
D1 ,
, 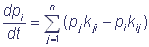 ; pi(0) = bi (i = 1, 2, ..., n), где bi - начальные значения вероятностей соответствующих состояний.
; pi(0) = bi (i = 1, 2, ..., n), где bi - начальные значения вероятностей соответствующих состояний.
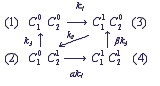 (2)
(2)
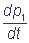 = k3 p2 - k1 p1;
= k3 p2 - k1 p1;
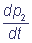 = k2 p3 - (k1 + k3) p2;
= k2 p3 - (k1 + k3) p2;
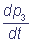 = k1 p1 + k3 p4 - k2 p3;
= k1 p1 + k3 p4 - k2 p3;
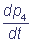 = k1 p2 - k3 p4; pi(0) = bi.
= k1 p2 - k3 p4; pi(0) = bi.