Russian
QUANTUM-CLASSICAL MODEL OF ELECTRON TRANSFER
The quantum-classical model presents the transfer of a charge (electron or hole) along a chain, which is built-up of several so called sites. Each of these sites corresponds to a harmonic oscillator. In the nature the double-stranded polymeric DNA molecule serves as example of such chain. In the DNA molecule monomers, which are complementary nucleotide pairs, are bonded among one another by covalent bonds. Nucleotide bases, which form a complementary pair, are bonded among one another by hydrogen bonds. The model considers interaction between the quantum (a charge) and classical (nucleotide base pair) systems. The DNA molecule resembles a solid body, as base pairs are stacked in it like in a crystal. But this is a linear crystal, as if it was one-dimensional: each base pair has only two closest nieghbours. The main difference of the DNA crystal from ordinary ones is its aperiodicity, as the sequence of base pairs in it is non-regular.
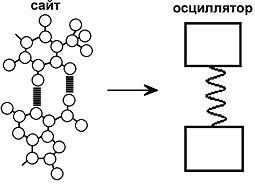 In the model under investigation a DNA fragment is considered as a chain, which consists of N sites. Each site corresponds to a nucleotide pair, which behaves like a harmonic oscillator. A hydrogen bond acts as a spring. In the model it is assumed that the nucleotide base planes are parallel to one another, and the distances between base planes of neighbouring sites are constant; this corresponds to B-DNA. A DNA molecule, while in the equilibrium state, does not have free charge carriers. Free electrons (anion-radicals) or holes (cation radicals) can be obtained either by photoexcitation or by chemical reactions.
In the model under investigation a DNA fragment is considered as a chain, which consists of N sites. Each site corresponds to a nucleotide pair, which behaves like a harmonic oscillator. A hydrogen bond acts as a spring. In the model it is assumed that the nucleotide base planes are parallel to one another, and the distances between base planes of neighbouring sites are constant; this corresponds to B-DNA. A DNA molecule, while in the equilibrium state, does not have free charge carriers. Free electrons (anion-radicals) or holes (cation radicals) can be obtained either by photoexcitation or by chemical reactions.
Charge transfer in a DNA is determined by overlapping
of nucleotide wave functions on neighbouring sites. If this transfer goes on along
one of DNA chains, then the overlapping integrals practically do not depend
on values of intersite displacements. Taking into account
that the nucleotide mass exceeds by several orders the electron mass, nucleotide
pair displacements can be described by classical equations of motion, and the expansion
of the charge can be described by quantum-mechanical ones. The Hamiltonian
of the charge transfer along the chain of sites has the form:
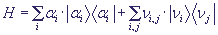 ,
(1)
,
(1)
where αi is the electron energy on the i-th site
with wave function  , ,
, , 
νi,j are matrix elements of transfer from the i-th to the j-th site. To describe the excitation transfer we will seek the solution of the Schroedinger equation:
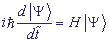 , (2)
, (2)
choosing a wave function in the form 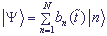 .
Value bn is the probability amplitude of location of the electron on the n-th site (
.
Value bn is the probability amplitude of location of the electron on the n-th site (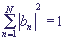 ).
).
We assume that the energy of an electron at the n-th site is a linear function of site displacements 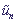 from their balanced states:
from their balanced states:
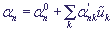 . (3)
. (3)
Inserting expressions for H, Ψ and αn into the Schroedinger equation and taking into consideration that νi,j = (νi,j)* = νj,i, i ≠ j (assuming all coefficients to be real numbers), we obtain:
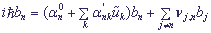 , n = 1,...,N, (4).
, n = 1,...,N, (4).
In the absence of dynamical fluctuations (when α'nk = 0) the system (4) describes coherent motion of the charge. In the general case site motions must not be neglected. In the model under investigation we assume that connection of the energy of the hole and displacement is weak enough; so, we consider in (3) only the linear term of expansion.
We restricted our consideration of dependence on displacements only to studying of diagonal matrix elements αn by virtue of the chosen geometry of the model. It stands to reason that in the general case we must also consider the nondiagonal matrix elements ηn,j dependence on site displacements; this dependence can make contribution of the same order. Moreover, in some cases it is precisely contribution of site displacement into nondiagonal part of the Hamiltonian, which is the major one.
The displacements 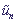 , which are included into system (4), must be defined from classical motion equations. To obtain these equations let us introduce kinetic energy of sites
, which are included into system (4), must be defined from classical motion equations. To obtain these equations let us introduce kinetic energy of sites  , Mk is the mass of the k-th site, and potential energy
, Mk is the mass of the k-th site, and potential energy 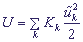 , Kk is elastic constant. The complete state-averaged Hamiltonian H of the system under investigation has the form:
, Kk is elastic constant. The complete state-averaged Hamiltonian H of the system under investigation has the form:
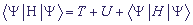 , (5).
, (5).
Having combined equations (4) and equations of motion for the Hamiltonian (5) we obtain a system of coupled equations, which determines charge distribution along N-site chain:
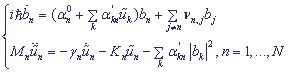 , (6).
, (6).
To take into account dissipation processes here, we introduced component γn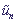 , γn is the frictional coefficient.
, γn is the frictional coefficient.
This system is self-consisted: evolution of probability amplitudes bn is determined by site displacements 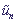 , which, in their turn, depend on the probability distribution |bn|2. Introducing of damping into the classical subsystem (6), generally speaking, is not necessary. Another way of modelling of similar effects on finite intervals of time is introducing of a large number of classical degrees of freedom for considering the model in detail, including into consideration separate atoms that are involved into the structure of the DNA, and molecules of solvent environment.
, which, in their turn, depend on the probability distribution |bn|2. Introducing of damping into the classical subsystem (6), generally speaking, is not necessary. Another way of modelling of similar effects on finite intervals of time is introducing of a large number of classical degrees of freedom for considering the model in detail, including into consideration separate atoms that are involved into the structure of the DNA, and molecules of solvent environment.
Henceforward we confine ourselves to the case of contact interaction: α'nk = δnkα'n, and assume that only the nearest neighbours of a site influence the dynamics of the site, that is, νi,j = 0, i ≠j ±1.; δnk is the Kronecker symbol here. The equations, which correspond to the system (6), have the form:
 , (7).
, (7).
The model, which has been introduced in such a way, is the simplest one describing dynamics of charge transfer in the DNA. The corresponding system in dimensionless variables has the form:
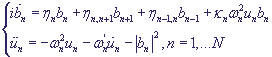 , (8).
, (8).
where τ = 10-14 is the characteristic time,
Un is the characteristic oscillation scale of the n-th site and
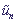 = Unun.
= Unun.
Let us require fulfilment of the ratio α'nτ2/MnUn = 1, that is Un = α'nτ2/Mn depends on the site mass and the energy of an electron on the site, and ωn is the oscillation frequency of the n-th site,
ηn = τα0n /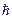 ,
ηn,n±1 = τνn,j /
,
ηn,n±1 = τνn,j / ,
ω2n = τ2Kn / Mn ,
ω'n = τγn / Mn ,
κn = α'nUnτ /
,
ω2n = τ2Kn / Mn ,
ω'n = τγn / Mn ,
κn = α'nUnτ / .
.
The effective mass of all sites is considered to be the same and equal to Mn = 10-21 g. High-frequency intermolecular oscillations in DNA, responding to oscillations of bases in a single site, have frequencies of picosecond order. Frequencies and frictional coefficients on sites are considered to be equal; the dimentionless values, which are corresponding to them, lie in the range: ω2 < In ≈ 10-4 - 10-6, ω'n ≈ 10-2 - 10-5.
© Lakhno V.D.
Supplementary information
N.S.Fialko, V.D.Lakhno.
Long-range charge transfer in DNA.
Regular & Chaotic Dynamics, 2002, 7 (3)
V.D.Lakhno.
Sequence dependent hole evolution in DNA.
Journal of Biological Physics, 2004, 30, 123-138
В.Д.Лахно, В.Б.Султанов.
Прыжковый и суперобменный механизмы переноса заряда в ДНК.
Биофизика, 2003, 48 (5), 797-801
| |
 In the model under investigation a DNA fragment is considered as a chain, which consists of N sites. Each site corresponds to a nucleotide pair, which behaves like a harmonic oscillator. A hydrogen bond acts as a spring. In the model it is assumed that the nucleotide base planes are parallel to one another, and the distances between base planes of neighbouring sites are constant; this corresponds to B-DNA. A DNA molecule, while in the equilibrium state, does not have free charge carriers. Free electrons (anion-radicals) or holes (cation radicals) can be obtained either by photoexcitation or by chemical reactions.
In the model under investigation a DNA fragment is considered as a chain, which consists of N sites. Each site corresponds to a nucleotide pair, which behaves like a harmonic oscillator. A hydrogen bond acts as a spring. In the model it is assumed that the nucleotide base planes are parallel to one another, and the distances between base planes of neighbouring sites are constant; this corresponds to B-DNA. A DNA molecule, while in the equilibrium state, does not have free charge carriers. Free electrons (anion-radicals) or holes (cation radicals) can be obtained either by photoexcitation or by chemical reactions.
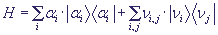 ,
(1)
,
(1)  , ,
, , 
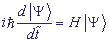 , (2)
, (2)
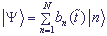 .
Value bn is the
.
Value bn is the 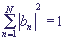 ).
).
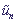 from their balanced states:
from their balanced states:
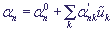 . (3)
. (3)
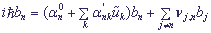 , n = 1,...,N, (4).
, n = 1,...,N, (4).
 , Mk is the mass of the k-th site, and potential energy
, Mk is the mass of the k-th site, and potential energy 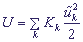 , Kk is elastic constant. The complete state-averaged Hamiltonian H of the system under investigation has the form:
, Kk is elastic constant. The complete state-averaged Hamiltonian H of the system under investigation has the form:
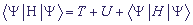 , (5).
, (5).
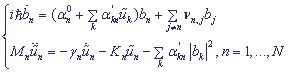 , (6).
, (6).
 , (7).
, (7).
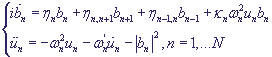 , (8).
, (8).
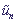 = Unun.
= Unun.
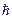 ,
ηn,n±1 = τνn,j /
,
ηn,n±1 = τνn,j /