English
КВАНТОВО-КЛАССИЧЕСКАЯ МОДЕЛЬ ПЕРЕНОСА ЭЛЕКТРОНОВ
Квантово-классическая модель моделирует перенос электрона вдоль цепочки, составленной из нескольких звеньев (называемых сайтами), каждый из которых представляется гармоническим осциллятором. В природе в роли такой цепочки служит двухцепочечная полимерная молекула ДНК, в которой мономеры - комплементарные нуклеотидные пары - связаны друг с другом посредством ковалентных связей. Нуклеотидные основания, образующие комплементарную пару, связаны между собой водородными связями. Модель учитывает взаимодействие между квантовой (заряд) и классической (нуклеотидные основания) системами. Молекула ДНК похожа на твёрдое тело тем, что пары оснований уложены в ней как в кристалле. Но это кристалл линейный, как бы одномерный - каждая пара оснований имеет только двух ближайших соседей. Основным отличием кристалла ДНК от обычных является его апериодичность, так как последовательность пар оснований в нём нерегулярна.
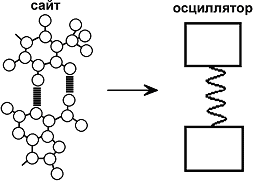 В исследуемой модели фрагмент ДНК рассматривается как цепочка, составленная из N сайтов. Каждый сайт представляет нуклеотидную пару, которая ведет себя как гармонический осциллятор. В роли пружины - водородная связь. В рассматриваемой модели считается, что плоскости оснований нуклеотидов параллельны друг другу, а расстояния между плоскостями оснований соседних сайтов постоянны, что соответствует B-форме ДНК. Молекула ДНК в равновесном состоянии не имеет свободных носителей заряда. Свободные электроны (анион-радикалы) или дырки (катион-радикалы) могут быть созданы либо посредством фотовозбуждения, либо в результате химических реакций.
В исследуемой модели фрагмент ДНК рассматривается как цепочка, составленная из N сайтов. Каждый сайт представляет нуклеотидную пару, которая ведет себя как гармонический осциллятор. В роли пружины - водородная связь. В рассматриваемой модели считается, что плоскости оснований нуклеотидов параллельны друг другу, а расстояния между плоскостями оснований соседних сайтов постоянны, что соответствует B-форме ДНК. Молекула ДНК в равновесном состоянии не имеет свободных носителей заряда. Свободные электроны (анион-радикалы) или дырки (катион-радикалы) могут быть созданы либо посредством фотовозбуждения, либо в результате химических реакций.
Перенос дырки в ДНК определяется перекрытием её волновых функций на соседних сайтах. Если перенос происходит вдоль одной из цепей ДНК, то интегралы перекрытия практически не зависят от внутрисайтовых смещений, независимо от величины последних. С учётом того, что масса нуклеотида на несколько порядков превышает массу дырки, смещения нуклеотидных пар можно описывать с помощью классических уравнений движения, а распространение дырки - квантово-механических. Гамильтониан переноса заряда вдоль цепочки сайтов имеет вид:
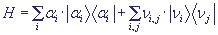 , (1)
, (1)
где αi - энергия электрона на i -ом сайте с волновой функцией  ,
,
νi,j - матричные элементы перехода с i -го на j -й сайт,  . Для описания переноса возбуждения будем искать решение уравнения Шредингера:
. Для описания переноса возбуждения будем искать решение уравнения Шредингера:
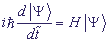 , (2)
, (2)
выбирая волновую функцию в виде 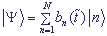 .
Величина bn представляет собой амплитуду вероятности нахождения электрона на n -ом сайте (
.
Величина bn представляет собой амплитуду вероятности нахождения электрона на n -ом сайте (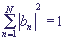 ).
).
Предполагаем, что энергия электрона на n -ом сайте является линейной функцией смещений сайтов 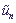 из их равновесных положений:
из их равновесных положений:
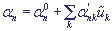 . (3)
. (3)
Подставляя выражения для H, Ψ и αn в уравнение Шредингера и учитывая, что νi,j = (νi,j)* = νj,i, i ≠ j (считая, что все коэффициенты - действительные числа), получаем:
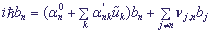 , n = 1,...,N, (4).
, n = 1,...,N, (4).
В отсутствии динамических флуктуаций (при α'nk = 0) система (4) описывает когерентное движение дырки. В общем случае движениями сайтов пренебрегать нельзя. В рассматриваемой модели мы предполагаем, что связь энергии дырки и смещений достаточно слабая, и учитываем в (3) только линейный член разложения.
Мы ограничились рассмотрением зависимости от смещений только диагональных матричных элементов αn в силу выбранной геометрии модели. Разумеется, в общем случае мы должны также учитывать и зависимость от смещений сайтов недиагональных матричных элементов ηn,j , которая может давать вклад такого же порядка. Более того, в ряде случаев именно вклад от смещений сайтов в недиагональную часть гамильтониана является основным.
Входящие в систему (4) смещения 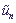 должны определяться из классических уравнений движения. Для получения этих уравнений введем кинетическую энергию сайтов
должны определяться из классических уравнений движения. Для получения этих уравнений введем кинетическую энергию сайтов  , Mk - масса k-го сайта, и потенциальную энергию
, Mk - масса k-го сайта, и потенциальную энергию 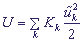 , Kk - упругая постоянная. Полный гамильтониан H рассматриваемой системы, усредненный по состоянию , имеет вид:
, Kk - упругая постоянная. Полный гамильтониан H рассматриваемой системы, усредненный по состоянию , имеет вид:
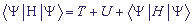 , (5).
, (5).
Объединяя уравнения (4) и уравнения движения для гамильтониана (5), получаем связанную систему уравнений, определяющую распределение заряда по N-сайтовой цепочке:
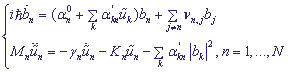 , (6).
, (6).
Здесь для учета процессов диссипации мы ввели член γn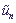 , γn - коэффициент трения.
, γn - коэффициент трения.
Эта система является самосогласованной: эволюция амплитуд вероятностей bn определяется смещениями сайтов 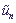 , которые, в свою очередь, зависят от распределения вероятностей |bn|2. Введение затухания в классическую подсистему (6) не является, вообще говоря, необходимым. Другой путь для моделирования подобных эффектов на конечных временах - введение большого числа классических степеней свободы для детализации модели, включая в рассмотрение отдельные атомы, входящие в состав ДНК, и молекулы окружающего ее растворителя.
, которые, в свою очередь, зависят от распределения вероятностей |bn|2. Введение затухания в классическую подсистему (6) не является, вообще говоря, необходимым. Другой путь для моделирования подобных эффектов на конечных временах - введение большого числа классических степеней свободы для детализации модели, включая в рассмотрение отдельные атомы, входящие в состав ДНК, и молекулы окружающего ее растворителя.
В дальнейшем мы ограничиваемся случаем контактного взаимодействия: α'nk = δnkα'n, и предполагаем, что на динамику поведения сайта влияют только его ближайшие соседи, т.е. νi,j = 0, i ≠j ±1.Здесь δnk - символ Кронекера. Уравнения, соответствующие системе (6), имеют вид:
 , (7).
, (7).
Введённая таким образом модель является простейшей моделью, описывающей динамику переноса заряда в ДНК.
Соответствующая система в безразмерных переменных имеет вид:
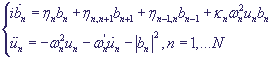 , (8).
, (8).
где τ = 10-14 - характерное время,
Un - характерный масштаб колебаний n -го сайта и
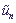 = Unun.
= Unun.
Потребуем выполнения соотношения α'nτ2/MnUn = 1, т.е.
Un = α'nτ2/Mn зависит от массы сайта и энергии электрона на сайте, а ωn - частота колебаний n -го сайта,
ηn = τα0n /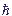 ,
ηn,n±1 = τνn,j /
,
ηn,n±1 = τνn,j / ,
ω2n = τ2Kn / Mn ,
ω'n = τγn / Mn ,
κn = α'nUnτ /
,
ω2n = τ2Kn / Mn ,
ω'n = τγn / Mn ,
κn = α'nUnτ / .
.
Эффективная масса всех сайтов считается одинаковой и равной Mn = 10-21 г.
Высокочастотные внутримолекулярные колебания в ДНК, отвечающие колебаниям оснований в отдельном сайте,
имеют частоты порядка пикосекунд.
Частоты и коэффициенты трения на сайтах считаются одинаковыми; соответствующие безразмерные величины лежат в диапазоне:
ω2n ≈ 10-4 - 10-6, ω'n ≈ 10-2 - 10-5.
© В.Д.Лахно
Дополнительная информация
N.S.Fialko, V.D.Lakhno.
Long-range charge transfer in DNA.
Regular & Chaotic Dynamics, 2002, 7 (3)
V.D.Lakhno.
Sequence dependent hole evolution in DNA.
Journal of Biological Physics, 2004, 30, 123-138
�.�.�����, �.�.��������.
��������� � ������������� ��������� �������� ������ � ���.
���������, 2003, 48 (5), 797-801
| |
 В исследуемой модели фрагмент ДНК рассматривается как цепочка, составленная из N сайтов. Каждый сайт представляет нуклеотидную пару, которая ведет себя как гармонический осциллятор. В роли пружины - водородная связь. В рассматриваемой модели считается, что плоскости оснований нуклеотидов параллельны друг другу, а расстояния между плоскостями оснований соседних сайтов постоянны, что соответствует B-форме ДНК. Молекула ДНК в равновесном состоянии не имеет свободных носителей заряда. Свободные электроны (анион-радикалы) или дырки (катион-радикалы) могут быть созданы либо посредством фотовозбуждения, либо в результате химических реакций.
В исследуемой модели фрагмент ДНК рассматривается как цепочка, составленная из N сайтов. Каждый сайт представляет нуклеотидную пару, которая ведет себя как гармонический осциллятор. В роли пружины - водородная связь. В рассматриваемой модели считается, что плоскости оснований нуклеотидов параллельны друг другу, а расстояния между плоскостями оснований соседних сайтов постоянны, что соответствует B-форме ДНК. Молекула ДНК в равновесном состоянии не имеет свободных носителей заряда. Свободные электроны (анион-радикалы) или дырки (катион-радикалы) могут быть созданы либо посредством фотовозбуждения, либо в результате химических реакций.
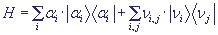 , (1)
, (1)
 ,
,  . Для описания переноса возбуждения будем искать решение
. Для описания переноса возбуждения будем искать решение 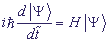 , (2)
, (2)
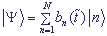 .
Величина bn представляет собой
.
Величина bn представляет собой 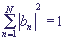 ).
).
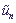 из их равновесных положений:
из их равновесных положений:
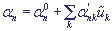 . (3)
. (3)
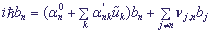 , n = 1,...,N, (4).
, n = 1,...,N, (4).
 , Mk - масса k-го сайта, и потенциальную энергию
, Mk - масса k-го сайта, и потенциальную энергию 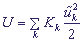 , Kk - упругая постоянная. Полный гамильтониан H рассматриваемой системы, усредненный по состоянию , имеет вид:
, Kk - упругая постоянная. Полный гамильтониан H рассматриваемой системы, усредненный по состоянию , имеет вид:
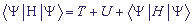 , (5).
, (5).
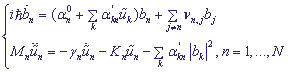 , (6).
, (6).
 , (7).
, (7).
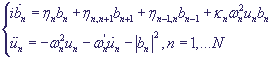 , (8).
, (8).
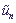 = Unun.
= Unun.
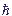 ,
ηn,n±1 = τνn,j /
,
ηn,n±1 = τνn,j /