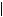Ψi(x, y, z)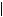2 для данного состояния i в точке (x, y, z) дает вероятность нахождения электрона в объеме dxdydz: pi(x, y, z) = 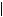Ψi(x, y, z)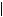2dxdydz.
ВОЛНОВАЯ ФУНКЦИЯ
Согласно квантово-механической теории, положение электрона в пространстве описывается волновой функцией Ψ(x, y, z), зависящей от пространственных координат x, y, z. Волновую функцию называют еще пси-функцией. Квадрат абсолютной величины волновой функции 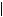Ψi(x, y, z)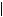2 для данного состояния i в точке (x, y, z) дает вероятность нахождения электрона в объеме dxdydz: pi(x, y, z) = 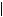Ψi(x, y, z)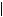2dxdydz.
Состояния, в которых энергия частицы E имеет определенные значения, называются стационарными состояниями. Такие состояния описываются волновыми функциями стационарных состояний ψn. Для волновых функций стационарных состояний справедливо уравнение Шредингера для стационарных состояний:
ψn = Eψn.
Здесь E - энергия частицы: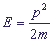 
, где p - импульс частицы, m - ее масса.
Произвольная волновая функция может быть разложена по волновым функциям стационарных состояний:
.
Для произвольной волновой функции уравнение Шредингера имеет вид:
.
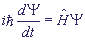- гамильтониан свободно движущейся частицы.