ОБЗОРЫ

ЛАХНО В.Д. "О КОНЦЕПЦИИ МАТЕМАТИЧЕСКОЙ КЛЕТКИ"

Огромное количество информации о строении и функционировании биологических систем поставило вопрос о создании математической модели элементарного кирпичика жизни - биологической клетки. Скорость накопления информации в биологии превышает соответствующую скорость в физике, химии и других науках. Компьютерная биология становится одним из наиболее приоритетных направлений среди других наук. Создание единой математической модели клетки кажется вполне созревшей задачей. Трудности в решении проблемы связаны со значительной сложностью постановки и проведения биологических экспериментов in vivo, необходимых для выяснения структуры и конкретных параметров такой модели, с недостаточной проработкой ее принципов с позиций теоретической биологии.

Моделирование клетки in silico должно учитывать постоянное эволюционное согласование внутриклеточных механизмов с характером функционирования клетки, адекватного изменениям внешней среды. Ключевым вопросом, на который должна давать ответ модель, является: можем ли мы точно предсказать, каков будет отклик клетки на изменение воздействия со стороны её окружения? Возможных практических результатов такого исследования можно придумать великое множество.

Чтобы подойти к постановке такой задачи, необходимо понять, на каком уровне описания физических явлений, происходящих в клетке, должна оперировать единая математическая модель. Клетка является макроскопическим объектом, в её состав входят сотни миллионов атомов. Отсюда, вытекает, что описание должно быть макроскопическим. Однако при нынешнем уровне знаний о микромире не вызывает сомнения тот факт, что функционирование клетки определяется процессами переноса заряда. Наиболее изученными являются процессы переноса в митохондриальной цепи электронного транспорта, в реакционном центре фотосинтеза, в нуклеотидных последовательностях, внутрибелковый и межбелковый перенос. Описание таких процессов является квантово-механическим. Таким образом, фундаментальная математическая модель должна базироваться на квантово-механическом описании. Это вполне соответствует современным представлениям о том, что в основе всех явлений, происходящих в природе, лежит квантовая теория. С этой фундаментальной точки зрения единой математической моделью всех явлений, включая живые системы, является оператор:

v_i₁i₂... ;j₁j₂...| i₁i₂...><j₁j₂...| (1)

действующий в гильбертовом пространстве, где i_k ( j_k ) - пробегающие как дискретные, так и непрерывные значения многомерные индексы с суммированием по повторяющимся индексам. Вся информация о мире в выражении (1) заключена в матричных элементах v_i₁i₂... ;j₁j₂..., а все функционирование мира заключено в динамических уравнениях для векторов состояний |i₁i₂...> и <j₁j₂...|.

В частности, все возможные пространственные структуры определяются решением спектральной задачи для оператора (1). На практике такой подход не применим даже при расчёте структуры одной белковой молекулы, ввиду неимоверной сложности решения такой задачи. Главное упрощение, позволяющее продвинуться в решении возникающих проблем, состоит в выделении отдельных подсистем. Для облегчения решения возникающей задачи в качестве подсистемы можно выбрать целую группу атомов или молекул, что при правильно сделанном выборе во многом предопределяет успех расчётов. Например, при изучении переноса одного электрона в рассматриваемой системе выделяют её фрагменты, называемые донор D и акцептор А. Согласно результатам теории химических реакций скорость перехода электрона с донора D на акцептор А определяется величиной матричного элемента H_DA:

H_DA = α_AiG_ij (E₀)α_jD

G_ij (E₀) = <i | (E₀ - v_i ^'_{j ^'} | i ^'><j ^'| )^-1 | j>, (2)

где в качестве донора выбран группа атомов с номером i = 0, а в качестве акцептора группа атомов с номером i = N + 1, G_ij -функция Грина для мостикового гамильтониана, из которого исключены донор и акцептор. В случае, когда речь идёт о макроскопических процессах, например конформационных переходах в белках, входящих в состав клеточной мембраны, динамические уравнения, определяемые (1), переходят в классические уравнения движения. Существует много способов последовательного перехода от квантовых уравнений к классическим, например, минуя квазиклассический уровень, переход на основе теоремы Эренфеста или основываясь на методе адиабатического приближения, использования модельных потенциалов и т.д. Если выделение классической подсистемы проведено, и переход к классическому описанию осуществлён, то дальнейшее продвижение на пути получения конкретных результатов связано с использованием численных методов. Наиболее эффективным подходом описания биомолекулярных систем является моделирование или имитация движения атомов и молекул, составляющих рассматриваемую систему. Такой подход носит название метода молекулярной динамики. В методе молекулярной динамики атомы и молекулы рассматриваются как классические частицы, взаимодействие между которыми считается известным. С помощью соответствующего метода вычислительной математики численно интегрируют уравнения движения классической механики для всех частиц системы при заданных потенциалах межчастичных взаимодействий и внешних полях:

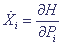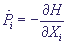; (3)

где X_i и P_i - координаты и импульсы частиц, входящих в систему. Рассмотренные случаи чисто квантового и чисто классического описания являются лишь крайними предельными случаями. Во многих случаях, например в процессах переноса электронов в клеточных структурах, необходимо ввести описание взаимодействия между квантовой (электрон) и классической (атомы или группы атомов) системами. Это достигается введением взаимодействия электрона с классическими степенями свободы, представляющими изменения положений атомов из равновесных положений при электронных переходах. С этой целью в матричных элементах выделяют компоненты, зависящие от классических переменных, полагая

α_ij = α_ij⁰ + α_{ij_k}u_k (4)

Изменение u_k во времени описывается классическими уравнениями движения. В итоге получаются самосогласованные квантово-классические уравнения движения, которые решаются с использованием достаточно мощных компьютеров. В тех случаях, когда удаётся разделить квантовую и классическую подсистемы и свести их описание к небольшому числу переменных, возникает вычислительная задача - решение систем самосогласованных динамических квантово-классических уравнений.

Весь транспорт зарядов в клетке можно условно разделить на два типа: транспорт внутри клеточных органелл и клеточной мембраны и транспорт между органеллами и различными участками клеточной мембраны. В первом случае заряд, например электрон, движется в гетерогенной среде, определяемой структурным устройством органелл. Во втором случае заряд транспортируется каким-либо носителем, например белком. Все метаболические процессы в клетке тесно связаны с процессами электронного переноса. Общие математические подходы к описанию этих процессов включают в себя суперобменный, прыжковый, поляронный, зонный (механизм молекулярной проволоки) и другие аналогичные современным подходам математического описания функциональной протеомики.

Наиболее просто, с использованием лишь классического подхода, моделируются процессы переноса заряда между органеллами. Например, участие в гликолизе NAD(P)H сопровождается переносом электрона NAD(P)H > Red с дальнейшим транспортом NAD(P)⁺ положительного заряда. Уравнения движения транспортёра заряда могут быть записаны в форме ланжевеновских уравнений:

(5)

где ω^'_n - коэффициент трения n-го транспортёра, f_n - случайная сила, воздействующая со стороны окружения на этот транспортёр. Таким образом, уравнение (5) описывает броуновскую динамику транспортёра. Если транспортёр несёт заряд, который при подходе на некоторое расстояние или непосредственном контакте с органеллой переходит на неё, то без всякой детализации процесса переноса заряда на органеллу, полученный результат может быть просто зафиксирован. С этого момента миграция заряда по органелле описывается другими уравнениями.

Если процесс перехода заряда при контакте транспортёра и органеллы по каким-либо причинам важен, его можно специально детально смоделировать. Соответственно, если к определённому участку органеллы подходит "пустой" транспортёр, то с этого участка заряд может перейти на транспортёр для его дальнейшего переноса. Весь запущенный процесс моделирования завершается по истечении времени, когда все разделённые изначально заряды используются в процессе создания продуктов жизнедеятельности клетки. Рассмотренное выше "прямое моделирование" транспортных процессов в компартментах клетки может на практике оказаться неэффективным ввиду большого числа идентичных транспортёров, вовлечённых в эти процессы. В этом случае вместо прямого моделирования можно перейти к статистическому описанию, а именно, к вытекающему из (5) уравнению Фоккера-Планка:

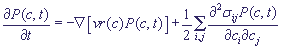(6)

где Р(с, t) - функция плотности вероятности; v -стехнометрическая матрица; r (с) - закон, определяющий скорость реакции, σ_ij - матрица, связанная со стохастическими процессами. Величина P(c,t)∂c - определяет вероятность найти клетку с концентрацией транспортёров в интервале [с, с+∂c] в момент времени t. На этом уровне описания основная трудность состоит в решении системы уравнений в частных производных, что представляет большие трудности, когда имеется несколько различных компонент, участвующих в процессах переноса.

Создание математической модели процессов, протекающих в живой клетке, открывает совершенно новые перспективы управления этими процессами. Основной проблемой создания единой модели клетки при условии полного знания всех важных составляющих этих процессов является их иерархия во времени и пространстве. На примере клетки высших растений видно, что пространственная организация клетки включает мембрану, которая является функциональной границей клетки. Ограниченное мембраной пространство заполнено цитоплазмой - функциональной средой, в которой расположены основные компоненты клетки - органеллы. Органеллы являются пространственно разделёнными образованиями со своими специализированными функциями. Все составляющие клетки находятся во взаимодействии, поддерживая её функционирование.

Процессы, происходящие в клетке, могут быть разделены в соответствии с их временными масштабами. Возможность разделения описания клетки по пространственной организации и временным масштабам процессов даёт шанс на поэтапное построение её математической модели. Бессмысленно конструировать единую математическую модель, имея в виду её практическую применимость, справедливую во всём рассматриваемом временном интервале.

Более подробно о концепции математической модели клетки см. статью В.Д. Лахно "Математическая клетка. Концепции построения математических моделей переноса заряда в живой клетке". Вестник РУДН, Серия Прикладная и компьютерная математика, 2003, т.2, No.2, с. 77-84.