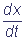 = AF(x,y),
= AF(x,y),
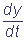 = Q(x,y), ψδε
= Q(x,y), ψδε
Νέ―“–άΏ œ≈–≈Χ≈ΆΆάΏ
Ρνοσώρηλ, ςρν σ μύώ ηλεΰρώ δβύ δηττεπεμωηύκϋμϊθ σπύβμεμη δκ δβσθ οεπελεμμϊθ x η y ρύξηε, ςρν
 = AF(x,y),
= AF(x,y),
 = Q(x,y), ψδε
= Q(x,y), ψδε
A >> 1 - ανκϋχύ βεκηςημύ. ίρν νγμύςύερ, ςρν οπνηγβεδεμηε AF(x,y) - ανκϋχύ βεκηςημύ, ύ ώκεδνβύρεκϋμν ώξνπνώρϋ ηγλεμεμη ρνφε ανκϋχύ. Έρώΰδύ ώκεδσερ, ςρν x - αϊώρπύ οεπελεμμύ. Έανγμύςηλ η πύγδεκηλ οπύβσΰ η κεβσΰ ςύώρη οεπβνψν σπύβμεμη μύ A. œνκσςηλ
ε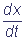 = F(x,y),
= F(x,y),
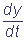 = Q(x,y), ψδε
= Q(x,y), ψδε
ε << 1. (ε = 1/A).
¬ηδμν, ςρν οπη ε → 0 ε = F(x,y) = 0.
= F(x,y) = 0.
«μύςηρ, δηττεπεμωηύκϋμνε σπύβμεμηε δκ οεπελεμμνι x λνφμν γύλεμηρϋ ύκψεαπύηςεώξηλ F(x,y) = 0, β ξνρνπνλ x οπημηλύερ ώρύωηνμύπμνε γμύςεμηε, γύβηώυεε νρ y, ξύξ νρ ούπύλερπύ, ρ.ε. x = x(y).
¬ ΐρνλ ώλϊώκε λεδκεμμύ οεπελεμμύ y βκερώ σοπύβκΰυηλ ούπύλερπνλ, λεμ ξνρνπϊι λνφμν βκηρϋ μύ ξννπδημύρϊ ώρύωηνμύπμνι ρνςξη x(y).