Quantum-classical model of excitation transfer along a DNA fragment is computed. This DNA fragment is considered to be a chain of N sites. Each of these sites behaves as a harmonic oscillator. It is conventional, that the base planes of nucleotides are parallel to one another, and the distance between base planes of neighbouring sites are constant; this corresponds to the B-form of DNA.
,
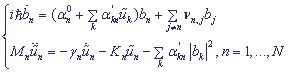where
bn is the probability amplitude of the electron localization at the n -th site,
α0n is the excitation energy at the n -th site,
α'n is coupling constant between the charge with nucleotides,
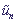are displacements of sites from their equilibrium positions,
νi,j are matrix elements of transition from the i -th to the j -th site,
Mk is the mass of the k -th site,
γk is the friction coefficient,
Kk is the elastic constant.
All derivatives are differentiated here with time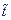 
.
Let τ = 10-14 sec is the characteristic time,
Un is the characteristic size of fluctuation of the n -th site,
that is 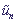= Unun, 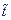= τ·t.
The corresponding system in proximity of the nearest neighbours in non-dimensional variables has the following form:
,
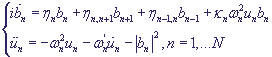The effective mass of all sites is considered to be the same, and it is equal to Mn = 10-21 g.
High frequency intramolecular oscillations in DNA, which correspond to oscillations of bases in a separate site, have frequencies of picosecond order. Frequencies and friction coefficients on sites are considered to be the same; the corresponding non-dimensional values lay in the range
ω2n ≈ 10-4 - 10-6, ω'n ≈ 10-2 - 10-5.
The system is solved by the fourth-order Runge-Kutta method with constant step.
,
ηn,n±1 = τνn,j / 